从原始的谈话到后来的书面文字,人们的生活需要通信。19世纪电报、电话出现以后,人类进入“电通信”时代,通信发生了根本性的变化,通信速度如“闪电”一样实时,通信空间可跨越高山大河、沙漠海洋。随着通信技术的快速发展和第二次世界大战的迫切需求,人们期待用一种理论来统一解释通信工程中取得的各种成果,并解决通信工程中的可靠性和有效性等问题。通信的可靠和高效是一对相互矛盾的现实要求,但可靠往往是第一位的,信息论就是在这样的背景下开启了这两个方面的定量研究。
通信定量关系的建立
通信问题的定量研究就是用数学方法建立一个模型,找出最基本的定量关系。香农认为,各种通信形式其过程可分为信源、发送器、信道、接收器和信宿等5个部分,通信的基本问题可归结为精确地或近似地在接收端重现发送端的消息(message)。为使通信的问题得到进一步简化,香农忽略了消息的具体内容,只考虑其形式,把通信中存在的语义问题和技术问题进行区别,从而得到了通信的一系列数学结论。1948年,香农在《贝尔系统技术学报》上分两期发表了论文《通信的数学理论》,标志着现代信息论的正式诞生。
●信息的数学定义
在此之前,人们认为通信过程与电力工程本质上是一样的,信源发出的消息可看作一种能展开成傅里叶级数或者傅里叶积分的时间函数。但是,香农认为信源发出的消息应该看成随机序列。例如,英文电报出现的消息可视作在字母表中一次一个地挑出字母(包括空格),字母出现的概率不相等,而后面字母出现的概率受前面字母的影响而发生变化。在数学上,这个过程可以用“马尔科夫过程”来描述。于是,香农把离散信源看作“马尔科夫过程”,认为信源是根据已知的(或在某种意义上可知的)概率从各种可能的消息中选择消息发出去的。他用“马尔科夫过程”的统计特性即它的熵来表征信源的特性,将它定义为该信源发送每个消息(符号)的平均信息量,它等于每个符号的概率的对数乘以其概率之积的总和,即
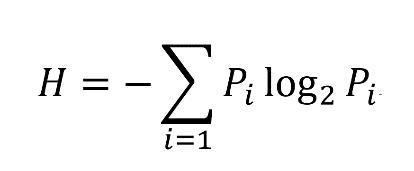
显然,当每个符号的概率相等时,平均信息量达到极大值。但是,在一般情况下,通信系统中都达不到这个最佳条件。香农把平均信息量和极大值的差与极大值的比称为该信源的冗余度,并指出可以通过对信源编码来改变这种有冗余度的输出,使信源与信道匹配,使信源上符号的平均信息量达到最大且等于信道容量,这也称为香农的“信源编码定理”。
●信道容量的测算
信号在信道中传输得越快,就越容易出错。同时,信号还会受到各式各样的噪声干扰。香农认为,噪声通常是随机出现的,噪声可视为与信号一起被集中发送而不失一般性。进一步研究表明,无论有无噪声,信道都存在一个容量问题,且只要信源发出消息的速度小于这个容量,信源的消息就能以任意小的差错率通过此信道,否则就会出现差错。香农用“疑义度”来量度这种差错。因此,信道容量就是能够几乎无误差地传送信息的最大速度,即

该公式给出了通信能力的理论极限值,任何通信系统只能通过编码或调制接近它,而不能达到它。几十年来,大家对这个理论结果虽质疑不断,但最终被证明是正确的。因此,寻找最佳信息编码和传输方式一直成为通信工程和信息论界的学术热点,也由此诞生了多址接入技术、多输入多输出技术、信道编码技术等多个技术。
●连续信道的信号处理
针对连续信道,香农对信号的处理分两步进行。先是采样,把连续时间信号转换为离散时间信号。然后是重建,把离散时间信号还原成连续时间信号。通信的统计概念早在香农之前已酝酿,美国数学家维纳(Norbert Wiener)、苏联数学家柯尔莫哥洛夫(Andrey N. Kolmogorov)以及英国统计学家费谢尔(Ronald A. Fisher)就曾先后提出过类似的想法。百分之百的重建信号,显然既无可能也无必要,只要接收的信号相当逼真即可。因此,香农还引入“可信度”作为接收者满意的标准。可信度的大小由接受者的要求高低来确定。
1949年,香农又发表了一篇划时代的论文《保密系统的通信理论》,开创了用信息理论研究密码的新途径,被后人公认为是现代密码学的里程碑。这个理论的意义在于,获得密文或没有获得密文,对满足香农完全保密性定理的保密系统而言是一样的,即具有“完全的保密性”,换句话说就是“香农意义下的不可破译性”。因此,设计不可破译密码系统成为密码学家一直努力的方向。当前区块链中所用的非对称公开密钥密码体制正是基于这样的思想,香农的信息论为区块链技术的诞生奠定了理论基础。
两个重要概念的确立
信息论中定量关系的建立,诠释了电报、电话等通信工程中所取得的成就,并解决了通信工程中遇到的可靠性和有效性等问题。同时,香农关于信息的概念和信息的测量单位“比特”的有关认识,仍然是理解当今数字时代的基石。
●信息概念的本质
“信息”是一个长期的高频词,常见于人们的日常谈话和各种新闻报道中,自20世纪七八十年代开始就已家喻户晓。但是,关于“信息到底是什么”,人们一直争议不断,甚至可以说混乱不堪。1975年,有人统计,有关信息的定义多达39种。即便是现在也是如此。造成这样的情况,一个重要的原因在于香农信息概念的抽象性与公众信息概念的直观性之间的矛盾。
从上面的叙述可以看出,香农要为通信工程建立一般性的数学模型,首先要做的就是去除其“意义”。对此,香农曾不无兴奋地说:“对信息论的研究而言,信息的‘意义’基本上无关。”对一个数学家来说,更重要的是定量把握基本的信息概念。香农曾进一步解释说:“这里的‘信息’虽然与这个词的日常意义有关,但不应该与其相混淆。”香农就是要去除其中的“心理因素”,而集中在“物理层面”,即信息是剥离了语义内容后剩下的“不确定性”,即熵。把香农“信息熵”和“统计力学熵”联系起来,是信息概念的主流认识。它们不仅形式一致(只差一个负号),而且有着内在的本质联系——信道定理可视为热力学第二定律在通信中的特殊形式。自然界封闭系统的熵不断增加而趋于无序,同样,通信过程只会趋于失真。因此,法国物理学家布里渊(Marcel Brillouin)认为,信息与热力学中的负熵等价,并以此解释了麦克斯韦妖(Maxwell’s demon,一种诙谐的假定)荒谬。他说:“如果麦克斯韦妖不接收信息就不能有序地工作,而如果不给某种类型的能量输入它就不能接收信息的控制。”有意思的是,维纳直接用负熵定义信息,而布里渊则认为没有必要。因此,信息在公众心中代表的是有序和确定,而在香农那里代表的是无序和不确定。
在科学家眼里,信息究竟是熵还是负熵,虽一直存在争论,但更多的是语义的理解和概念的解释。正如北京遥测技术研究所郝建民研究员所说:“信息概念在香农、维纳和布里渊手里,说是就是,不是也是;说不是就不是,是也不是。”不管怎样,信息从数学的视角来看,概念是确定的。1951年,“信息论”一词得到了英国无线电工程师协会的认可。1954年,英国无线电工程师协会在美国麻省理工学院召开了第一次信息论国际会议。同年,美国电子和电气工程师协会出版了信息论汇刊。至此,信息论作为一门学科正式确立下来。
●信息的基本单位
香农创造性地用概率的函数解决了信息的度量问题,并用了一个在当时看来颇为时尚的名字“熵”。熵作为信息的度量,自然需要一个单位。香农认为,如果以2为对数函数的底,相应结果的单位就可以称为二进制数字(binary digit),或简称比特(bit)。
比特作为信息最小的可能取值,1比特可代表投掷硬币出现正反面时的不确定程度。投掷硬币有两种可能,且出现的概率相等。在香农“信息熵”中,P1、P2都是1/2,而1/2以2为底的对数就是—1,因此,H的值就是1比特。从包含32个字符的字母表中随机挑选一个字符,那就是5比特,因为32以2为底的对数是5。以此类推,1 000个从包含32个字符的字母表中随机选出的字符,可能组成的信息数就是32的1 000次方,而这个数以2为底的对数就是5 000。
除了投掷硬币的两种可能表示1比特的方式外,关于比特,香农还提供了一种更为实用的例子:一个具有两个稳态的设备,如继电器或双稳态触发器,可以存储1比特信息。此类设备被组合在一起,如继电器阵列,就可以存储数百、数千信息。由于当时晶体管还没有被发明,这样存储的信息在当时来说已经很大。1949年,香农在笔记本上自上而下地画了1条竖线,依次写下10的0次方至10的13次方,并对应写出可用来“存储”信息的东西,如10的3次方下方写着“打孔卡片”,10的5次方下方写着“人类的基因构成”。需要说明的是,那时DNA结构还没有被发现,被誉为“DNA之父”的沃森(James D. Watson)还只是美国印第安纳大学动物学系的一名学生。可以说,这是人类首次提出基因是一个信息库,并可用比特来度量。尽管香农的大胆科学猜想比实际少了4个数量级,但是仍可说是史无前例的。香农创造性地把二进制数作为通信的基本单位,是信息发展史上的创举。目前,比特作为信息世界的最小单位,如同夸克目前成为物质世界的最小单位一样,被广泛使用,并不断借用到其他领域中。


